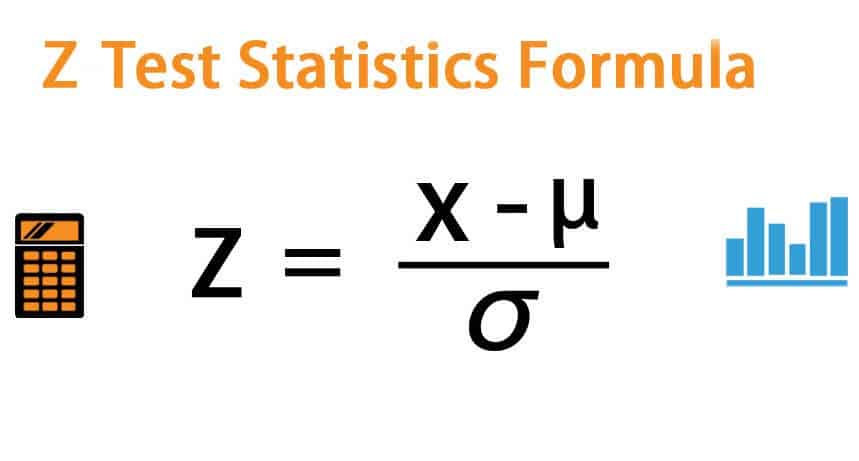Diferencia entre la prueba Z y el valor P (con tabla)

La prueba Z y el valor P son dos pruebas estadísticas, pero son dos cosas separadas en las que la primera es una prueba estadística que arroja luz sobre si se debe rechazar la hipótesis nula o no, mientras que la última es una prueba de probabilidad que significa que hay una probabilidad de que se rechace la hipótesis nula.

Una prueba Z en estadística es una herramienta que se utiliza para determinar si dos medias poblacionales varían incluso cuando se conocen las variables. Es un tipo de prueba de hipótesis bajo la hipótesis nula y se puede aproximar mediante una distribución normal.

Una prueba de hipótesis en estadística es una forma de averiguar si los resultados de una encuesta o experimento son significativos o no.

Considerando que, un valor P o el valor de probabilidad, en hipótesis estadística, es la probabilidad de obtener los resultados de la prueba / experimento observados durante la prueba o experimento con el supuesto de que la hipótesis nula es correcta.

Una hipótesis nula es una declaración general que indica que no existe relación entre los dos grupos medidos.

los diferencia entre la prueba Z y el valor P Esta prueba Z habla de si la hipótesis nula debe ser rechazada o no, pero por el contrario el valor P arroja luz sobre las observaciones que se han hecho durante el experimento si son iguales o extremas cuando la hipótesis nula es verdadera. .

Tabla de comparación entre la prueba Z y el valor P (en forma tabular)

Prueba Z del valor p básico

Sentido	El valor p es la probabilidad de que las observaciones permanezcan iguales o extremas, si la hipótesis nula es cierta.	La prueba Z describe la desviación de la media en unidades de desviación estándar.
Supuestos	El valor P es la prueba llevada a cabo con el supuesto de que la hipótesis nula es verdadera.	En el caso de Z-Test, no hace tales suposiciones.
Objetivo	El objetivo de esta prueba es averiguar si la hipótesis nula debe aceptarse o no.	El objetivo de esta prueba es comprobar si las observaciones siguen siendo las mismas o no si la hipótesis nula es cierta.
Indicación de la prueba	El valor P indica cuán improbable es la estadística.	Considerando que, la prueba Z indica qué tan lejos está la media.

¿Qué es Z-Test?

Una prueba Z en estadística es una herramienta que se utiliza para determinar si dos medias poblacionales varían incluso cuando se conocen las variables. Además, el tamaño de la muestra es grande. Es un tipo de prueba de hipótesis bajo la hipótesis nula y se puede aproximar mediante una distribución normal.

Se utiliza para comprobar si la hipótesis nula debe rechazarse o no. Las puntuaciones Z son las medidas de la desviación estándar, por ejemplo, +1,95 o -1,95 denota cuánto se ha desviado el resultado de la estadística de la prueba de la media.

Hay algunas suposiciones que se realizan en la prueba Z de una muestra:

Los datos son continuos y no discretos.
Los datos siguen la distribución de probabilidad normal.
La muestra debe ser aleatoria; de lo contrario, es posible que el resultado de la estadística de prueba no sea correcto.
La desviación estándar de la población se conoce

¿Qué es el valor P?

El valor p es la probabilidad de que el resultado de la estadística de prueba sea rechazado o aceptado con el supuesto de que la hipótesis nula es correcta. El experimento establece el nivel de significancia y cuando el valor p es menor que el nivel significativo, la hipótesis nula será rechazada.

Para averiguar el valor p en la estadística de uno:

Busque la estadística de la distribución adecuada.
Encuentre la probabilidad de que la media esté más allá de su estadística de prueba.
Si la hipótesis es menor que la alternativa, entonces encuentre la probabilidad de que la media sea menor que su estadístico de prueba. Este es el valor p.
Si la hipótesis es mayor que la alternativa, entonces encuentre la probabilidad de que la media sea mayor que la estadística de prueba. Este es el valor p.
Si la hipótesis es igual a la alternativa, entonces necesitamos encontrar la probabilidad de que la media sea extrema para su estadística de prueba y duplicarla.

Principales diferencias entre la prueba Z y el valor P

Sentido

El valor P es la probabilidad de obtener un resultado estadístico de prueba al menos igual o tan extremo como el resultado observado en el experimento con el supuesto de que la hipótesis nula es verdadera.

Considerando que, la prueba Z es la prueba que se utiliza para determinar si la media de una población es mayor, menor o igual a un valor específico. Como utiliza la distribución normal estándar, esta prueba a menudo se conoce como Prueba Z de una muestra. Supone que se conoce la desviación estándar de la población.

Hipótesis nula

En el caso de P-Value, se asume que la hipótesis nula es verdadera, en base a lo cual se verifica el resultado de la estadística de prueba que se observa en el experimento para ver si el resultado es el mismo o extremo que se observó antes. Por otro lado, la prueba Z se utiliza para verificar si la hipótesis nula debe rechazarse o no.

Hipótesis alternativa

En el valor P, la hipótesis alternativa es la afirmación crucial que el experimentador quisiera concluir en la prueba experimental si los datos lo permiten. Mientras que, en la prueba Z, la hipótesis alternativa juega un papel importante junto con la hipótesis nula, alfa y el puntaje Z. La hipótesis alternativa es la hipótesis opuesta, es una afirmación de una diferencia en la población. Es la hipótesis que el experimentador espera probar.

Limitaciones

En el caso del valor p, el valor p podría no ser correcto si el tamaño de la muestra es pequeño. Además, el valor p tiene una tendencia a concluirse como significativo o no significativo en función del factor de que el valor p es menor o igual a 0,5, lo que no es el caso de la prueba Z; sin embargo, hay algunas limitaciones del uso de Z-Test.

El primero de los cuales es, el tamaño de la muestra puede variar desde un número pequeño hasta varios cientos. Si los datos son discretos con al menos cinco valores únicos, entonces se puede ignorar el supuesto de variable continua. Quizás la mayor restricción es que los datos deben ser aleatorios, de lo contrario, los niveles de significancia podrían ser incorrectos.

Resultados

Si el valor p es muy pequeño en comparación con el valor umbral que se eligió previamente conocido como nivel significativo (comúnmente 5% o 1%), sugiere que los datos observados son inconsistentes con el supuesto de que la hipótesis nula es verdadera y por tanto, la hipótesis debe ser rechazada y la hipótesis alternativa es aceptada.

Por ejemplo:

p <0,1, la hipótesis se rechaza
0.1
p & gt; 0.1, la hipótesis es aceptada

Considerando que, en Z-Test, para dar un ejemplo: Los valores críticos de Z-Score cuando se usa un nivel de confianza del 95%, -1,96 y +1,96 desviaciones estándar. El valor p asociado con un nivel de confianza del 95% es 0.05. Si su puntuación Z está entre -1,96 y +1,96, su valor p será mayor que 0,05 y no puede rechazar su hipótesis nula.

Si el puntaje Z cae fuera de ese rango (por ejemplo, -2.5 o +5.4), el patrón exhibido es probablemente demasiado inusual para ser solo otra versión del azar aleatorio y el valor p será pequeño para reflejar esto. En este caso, es posible rechazar la hipótesis.

Una idea clave aquí es que los valores en el medio de la distribución normal (puntuaciones Z como 0.19 o -1.2, por ejemplo), representan el resultado esperado

Conclusión

P-Value y Z-Test son dos pruebas estadísticas con diferentes objetivos. El valor P gira en torno a la probabilidad de que las observaciones o los resultados del experimento sean iguales o extremos si la hipótesis nula es cierta.

Por otro lado, la prueba Z significa la validez de las observaciones realizadas durante el experimento. Se usa solo cuando el tamaño muestral es mayor a 30 como en el caso de la población, es por el teorema central que se usa durante esta prueba, a medida que aumenta el número de muestras, se considera que las muestras están distribuidas normalmente y el los datos se seleccionan al azar.

El valor p se ve afectado por el tamaño de la muestra, así como por la hipótesis nula. Cuanto mayor es el tamaño de la muestra, más pequeños son los valores P, mientras que la prueba Z se ve afectada por la hipótesis nula, la hipótesis alternativa, el alfa y la puntuación Z.

Nube de palabras para diferenciar entre prueba Z y valor P

La siguiente es una recopilación de los términos más utilizados en este artículo sobre Prueba Z y valor P. Esto debería ayudar a recordar términos relacionados tal como se utilizan en este artículo en una etapa posterior.